Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в EXCEL

Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул MS EXCEL.

Начнем с определения, точнее с определений.

Чистой приведённой стоимостью (Net present value, NPV) называют сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню (взято из Википедии). Или так: Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт cfin. ru) Или так: Текущая стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика . Толковыйсловарь . — М . : « ИНФРА — М «, Издательство « ВесьМир «. Дж . Блэк .)

Примечание1 . Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется ЧПС() , то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с Приведенной стоимостью .

Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма Приведенных стоимостей денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.

Совет : при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи Приведенная стоимость .

Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу сложных процентов .

Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция ЧПС() (английский вариант — NPV()). В ее основе используется формула:

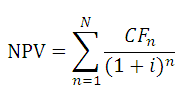
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).

Примечание2 . Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить: Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год) . Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).

Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV Примечание3 . Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.

Определившись со сроками денежных потоков, для функции ЧПС() нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см. файл примера, лист NPV ).

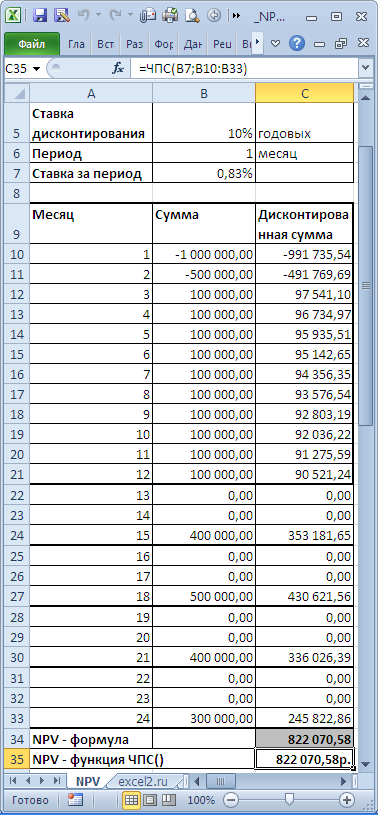
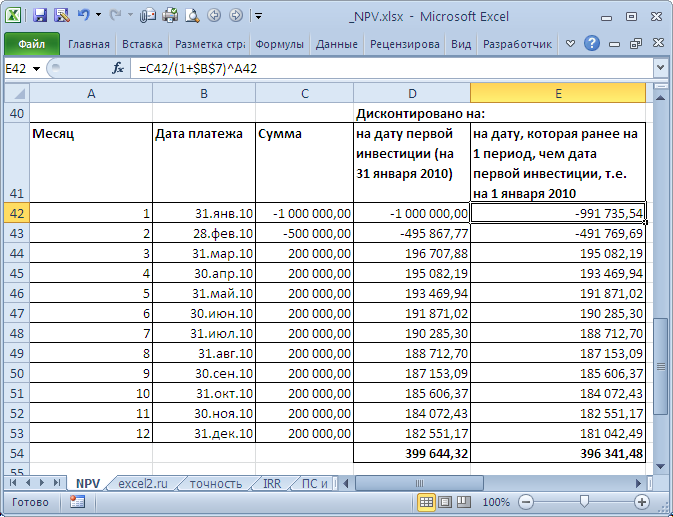
В таблице NPV подсчитан двумя способами: через функцию ЧПС() и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции ЧПС() , а нужно просто прибавить к получившемуся результату (см. файл примера ). Сравнение 2-х вариантов дисконтирования приведено в файле примера , лист NPV:

О точности расчета ставки дисконтирования

Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см. файл примера, лист Точность ).

Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.

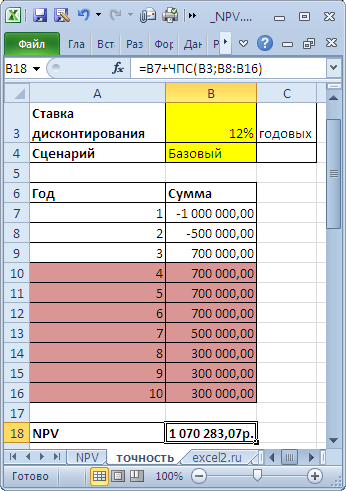
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):

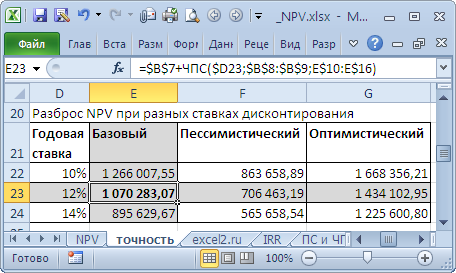
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.

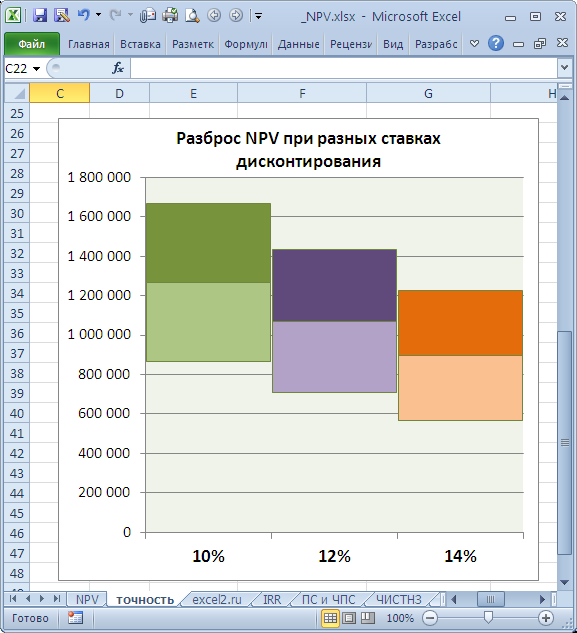
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.

Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0

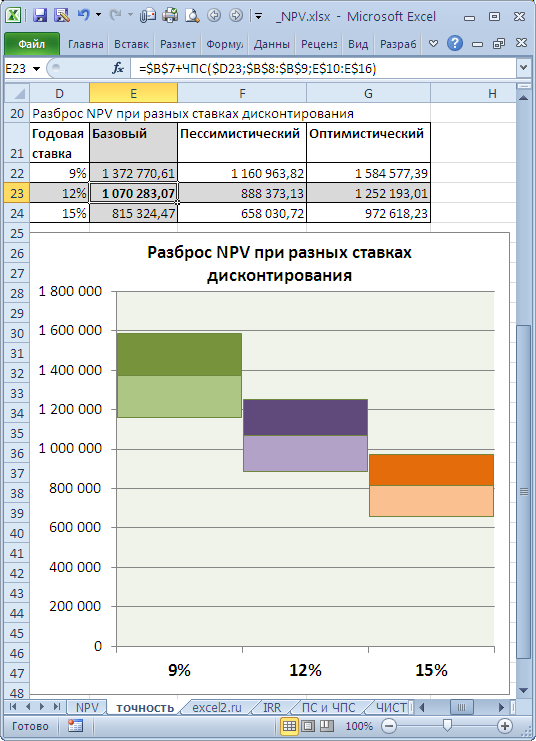
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.

Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.

После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.

Внутренняя ставка доходности IRR (ВСД)

Внутренняя ставка доходности (англ. internal rate of return , IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см. файл примера, лист IRR ).

Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.

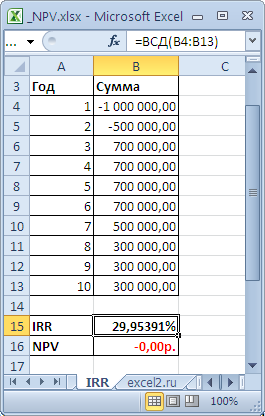
Для расчета IRR используется функция ВСД() (английский вариант – IRR()). Эта функция тесно связана с функцией ЧПС() . Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией ВСД() , всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле: =ЧПС(ВСД(B5:B14);B5:B14)

Примечание4 . IRR можно рассчитать и без функции ВСД() : достаточно иметь функцию ЧПС() . Для этого нужно использовать инструмент Подбор параметра (поле «Установить в ячейке» должно ссылаться на формулу с ЧПС() , в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).

Расчет NPV при постоянных денежных потоках с помощью функции ПС()

Напомним, что аннуитет представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию ПС() (см. файл примера, лист ПС и ЧПС ).

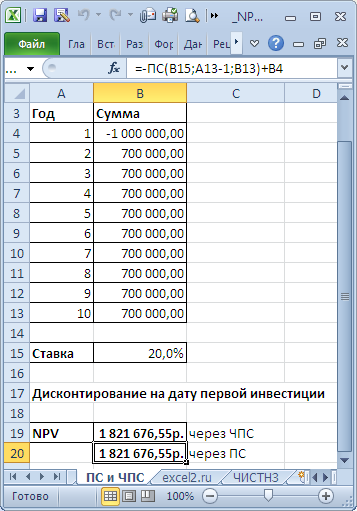
В этом случае все денежные потоки (диапазон В5:В13 , 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке В4 . Ставка дисконтирования расположена в ячейке В15 со знаком минус. В этом случае формула =B4+ЧПС(B15;B5:B13) дает тот же результат, что и = B4-ПС(B15;9;B13)

Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени

Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция ЧИСТНЗ() (английский вариант – XNPV()).

Функция ЧИСТНЗ() возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:

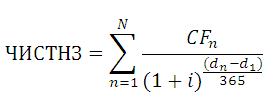
Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.

Принципиальным отличием от ЧПС() является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у ЧИСТНЗ() всегда годовая, т.к. указана база 365 дней, а не за период, как у ЧПС() . Еще отличие от ЧПС() : все денежные потоки всегда дисконтируются на дату первого платежа.

В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций ЧИСТНЗ() и ЧПС() . Эти функции возвращают несколько отличающиеся результаты. Для задачи из файла примера, Лист ЧИСТНЗ разница составила порядка 1% (период = 1 месяцу).

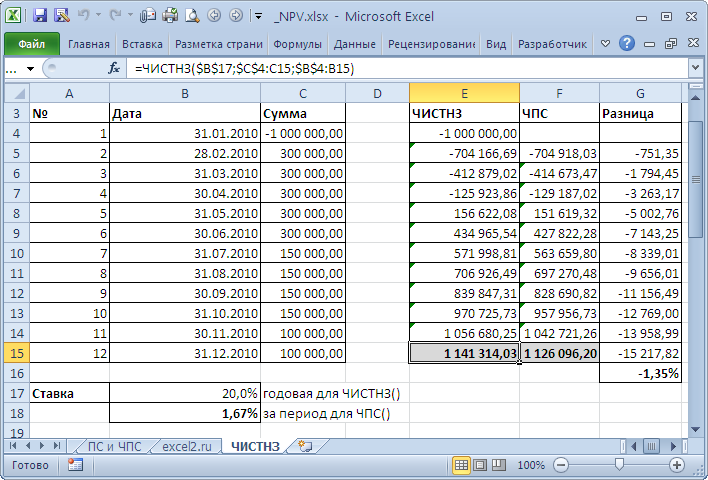
Это связано с тем, что у ЧИСТНЗ() длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у ЧПС() указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет високосного года).

Внутренняя ставка доходности ЧИСТВНДОХ()

По аналогии с ЧПС() , у которой имеется родственная ей функция ВСД() , у ЧИСТНЗ() есть функция ЧИСТВНДОХ() , которая вычисляет годовую ставку дисконтирования, при которой ЧИСТНЗ() возвращает 0.

Расчеты в функции ЧИСТВНДОХ() производятся по формуле:

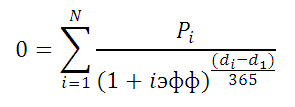
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).

Чистая приведенная стоимость — NPV

Определение

Метод чистой приведенной стоимости (англ. Net Present Value, NPV) получил широкое применение при бюджетировании капитальных вложений и принятии инвестиционных решений. Также NPV считается лучшим критерием отбора для принятия или отклонения решения о реализации инвестиционного проекта, поскольку основывается на концепции стоимости денег во времени. Другими словами, чистая приведенная стоимость отражает ожидаемое изменение благосостояния инвестора в результате реализации проекта.

Формула NPV

Чистая приведенная стоимость проекта является суммой настоящей стоимости всех денежных потоков (как входящих, так и исходящих). Формула расчета выглядит следующим образом:

Где CF_t – ожидаемый чистый денежный поток (разница между входящим и исходящим денежным потоком) за период t, r – ставка дисконтирования, N – срок реализации проекта.

Ставка дисконтирования

Важно понимать, что при выборе ставки дисконтирования должна быть учтена не только концепция стоимости денег во времени, но и риск неопределенности ожидаемых денежных потоков! По этой причине в качестве ставки дисконтирования рекомендуется использовать средневзвешенную стоимость капитала (англ. Weighted Average Cost of Capital, WACC), привлеченного для реализации проекта. Другими словами, WACC является требуемой нормой доходности на капитал, инвестированный в проект. Следовательно, чем выше риск неопределенности денежных потоков, тем выше ставка дисконтирования, и наоборот.

Критерий отбора проектов

Правило принятия решения об отборе проектов при помощи NPV метода довольно прямолинейно. Нулевое пороговое значение говорит о том, что денежные потоки проекта позволяют покрыть стоимость привлеченного капитала. Таким образом, критерии отбора можно сформулировать следующим образом:

1. Отдельно взятый независимый проект должен быть принят при положительном значении чистой приведенной стоимости или отклонен при отрицательном. Нулевое значение является точкой безразличия для инвестора.
2. Если инвестор рассматривает несколько независимых проектов, принять следует те из них, у которых наблюдается положительный NPV.
3. Если рассматривается ряд взаимоисключающих проектов, выбрать следует тот из них, у которого будет максимальная чистая приведенная стоимость.

Пример расчета

Компания рассматривает возможность реализации двух проектов, требующих одинаковых первоначальных инвестиций в размере 5 млн. у.е. При этом, оба обладают одинаковым риском неопределенности денежных потоков, и стоимостью привлечения капитала в размере 11,5%. Разница заключается в том, что по Проекту А основные поступление денежных потоков ожидаются раньше, чем по Проекту Б. Детальная информация об ожидаемых денежных потоках представлена в таблице.

Подставим имеющиеся данные в приведенную выше формулу рассчитаем значение чистой приведенной стоимости.

Дисконтированные денежные потоки по двум проектам представлены на рисунке ниже.

Если проекты являются независимыми, компания должна принять каждый из них. Если реализация одного проекта исключает возможность реализации другого, принять следует Проект А, поскольку он характеризуется более высоким NPV.

Расчет NPV в Excel

Рассчитать значение чистой приведенной стоимости можно также при помощи функции «ЧПС» в Excel, как показано на рисунке ниже.

1. Выберите ячейку вывода H6.
2. Нажмите кнопку fx, выберите категорию «Финансовые», а затем функцию «ЧПС» из списка.
3. В поле «Ставка» выберите ячейку C1.
4. В поле «Значение1», выберите диапазон данных C6:G6, оставьте пустым поле «Значение2» и нажмите кнопку OK.

Поскольку мы не учли первоначальные инвестиции, выберите ячейку вывода H6 и прибавьте ячейку B6 в строке формул.

Преимущества и недостатки метода чистой приведенной стоимости

Преимуществом метода NPV для при оценке проектов является использование методики дисконтированных денежных потоков, что позволяет оценить величину дополнительно создаваемой стоимости. Тем не менее, для этого метода характерны ряд недостатков и ограничений, которые необходимо учитывать при принятии решений.

1. Чувствительность к ставке дисконтирования. Одним из основных предположений является то, что все денежные потоки проекта реинвестируются по ставке дисконтирования. На самом деле, уровень процентных ставок постоянно меняется в следствие изменений экономических условий и ожиданий относительно уровня инфляции. При этом эти изменения могут носить значительный характер, особенно в долгосрочной перспективе. Таким образом, фактическое значение чистой приведенной стоимости может существенно отличаться от ее первоначальной оценки.
2. Денежные потоки после планируемого срока реализации. Некоторые проекты могут генерировать после запланированного срока реализации проекта. Эти денежные потоки могут обеспечить дополнительную стоимость к первоначальной оценке, но они игнорируются данным методом.
3. Управленческие опционы. В течение жизненного цикла проекта менеджмент компании может предпринять какие-либо действия, влияющие на сроки его реализации и масштаб в ответ на изменения рыночных условий. Эти действия могут изменить как время возникновения, так и величину ожидаемых денежных потоков, что приведет к изменению оценки чистой приведенной стоимости. Традиционный анализ дисконтированных денежных потоков не принимает во внимание такие изменения.

http://excel2.ru/articles/chistaya-privedennaya-stoimost-npv-chps-i-vnutrennyaya-stavka-dohodnosti-irr-vsd-v-ms-excel
http://allfi.biz/financialmanagement/CapitalBudgeting/chistaja-privedennaja-stoimost.php