Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в EXCEL
Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул MS EXCEL.
Начнем с определения, точнее с определений.
Чистой приведённой стоимостью (Net present value, NPV) называют сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню (взято из Википедии). Или так: Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт cfin. ru) Или так: Текущая стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика . Толковыйсловарь . — М . : « ИНФРА — М «, Издательство « ВесьМир «. Дж . Блэк .)
Примечание1 . Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется ЧПС() , то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с Приведенной стоимостью .
Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма Приведенных стоимостей денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.
Совет : при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи Приведенная стоимость .
Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу сложных процентов .
Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция ЧПС() (английский вариант — NPV()). В ее основе используется формула:
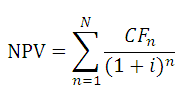
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).
Примечание2 . Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить: Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год) . Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).
Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV Примечание3 . Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.
Определившись со сроками денежных потоков, для функции ЧПС() нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см. файл примера, лист NPV ).
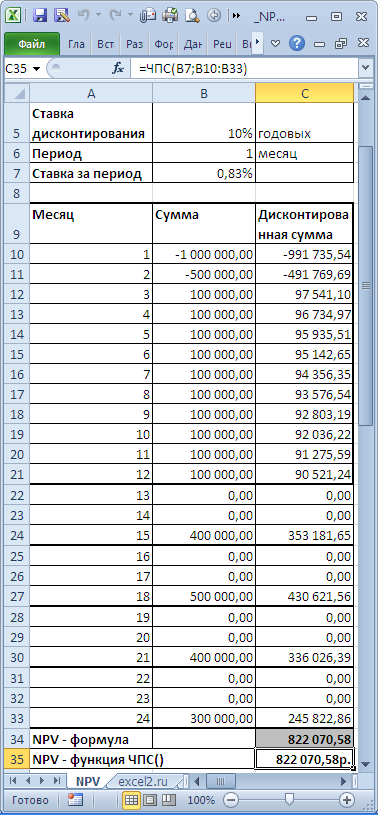
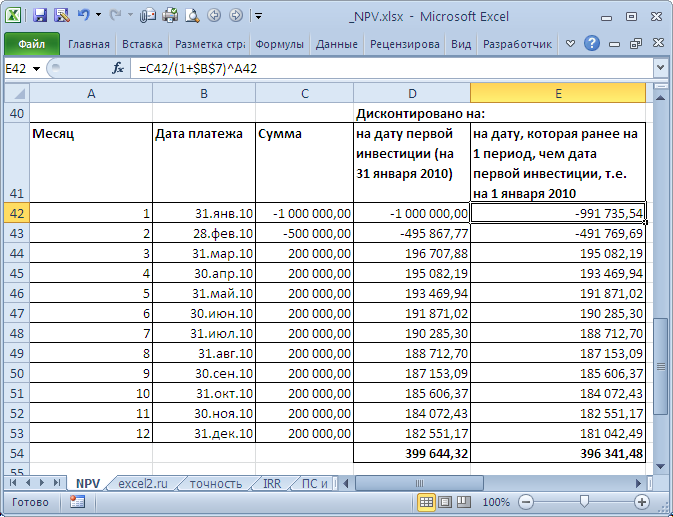
В таблице NPV подсчитан двумя способами: через функцию ЧПС() и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции ЧПС() , а нужно просто прибавить к получившемуся результату (см. файл примера ). Сравнение 2-х вариантов дисконтирования приведено в файле примера , лист NPV:
О точности расчета ставки дисконтирования
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см. файл примера, лист Точность ).
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
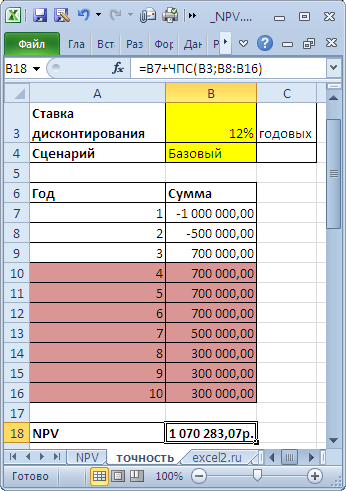
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
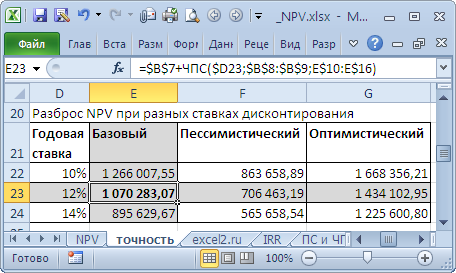
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
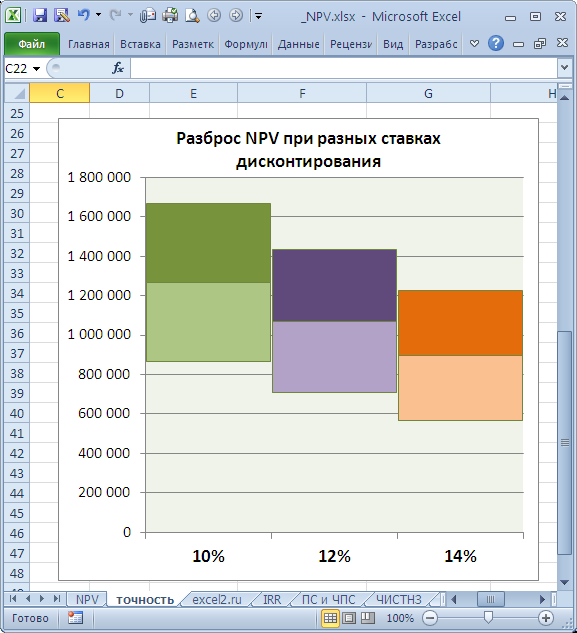
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0
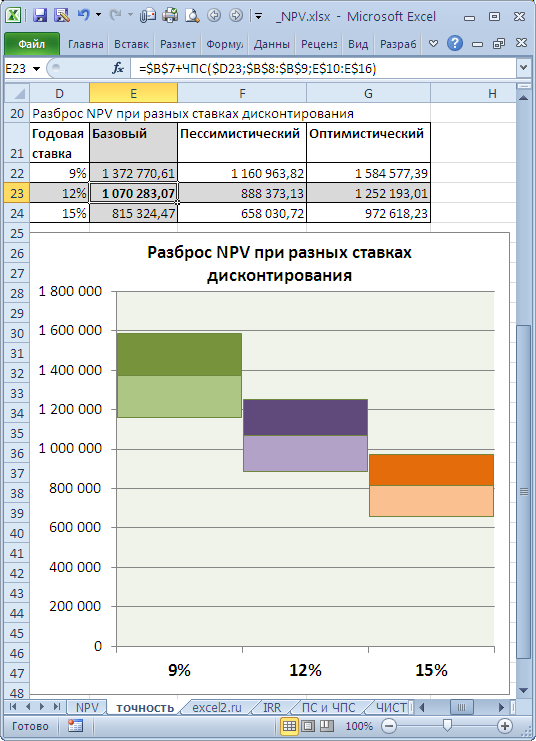
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.
Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.
После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.
Внутренняя ставка доходности IRR (ВСД)
Внутренняя ставка доходности (англ. internal rate of return , IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см. файл примера, лист IRR ).
Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.
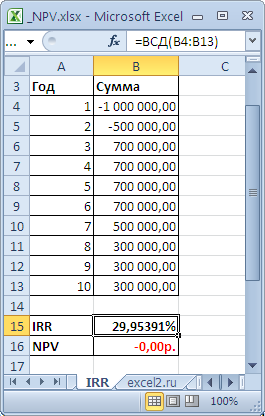
Для расчета IRR используется функция ВСД() (английский вариант – IRR()). Эта функция тесно связана с функцией ЧПС() . Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией ВСД() , всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле: =ЧПС(ВСД(B5:B14);B5:B14)
Примечание4 . IRR можно рассчитать и без функции ВСД() : достаточно иметь функцию ЧПС() . Для этого нужно использовать инструмент Подбор параметра (поле «Установить в ячейке» должно ссылаться на формулу с ЧПС() , в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).
Расчет NPV при постоянных денежных потоках с помощью функции ПС()
Напомним, что аннуитет представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию ПС() (см. файл примера, лист ПС и ЧПС ).
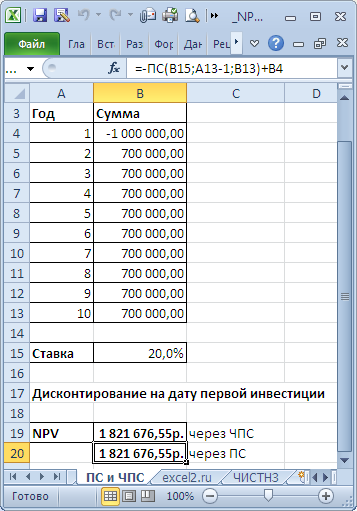
В этом случае все денежные потоки (диапазон В5:В13 , 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке В4 . Ставка дисконтирования расположена в ячейке В15 со знаком минус. В этом случае формула =B4+ЧПС(B15;B5:B13) дает тот же результат, что и = B4-ПС(B15;9;B13)
Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция ЧИСТНЗ() (английский вариант – XNPV()).
Функция ЧИСТНЗ() возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:
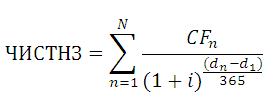
Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.
Принципиальным отличием от ЧПС() является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у ЧИСТНЗ() всегда годовая, т.к. указана база 365 дней, а не за период, как у ЧПС() . Еще отличие от ЧПС() : все денежные потоки всегда дисконтируются на дату первого платежа.
В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций ЧИСТНЗ() и ЧПС() . Эти функции возвращают несколько отличающиеся результаты. Для задачи из файла примера, Лист ЧИСТНЗ разница составила порядка 1% (период = 1 месяцу).
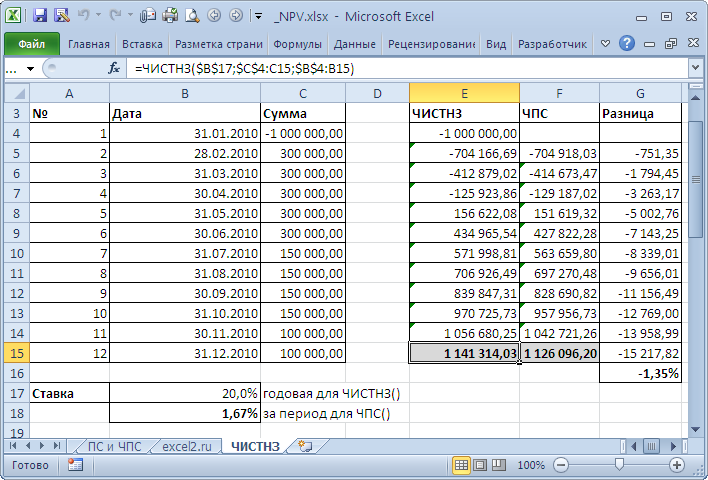
Это связано с тем, что у ЧИСТНЗ() длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у ЧПС() указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет високосного года).
Внутренняя ставка доходности ЧИСТВНДОХ()
По аналогии с ЧПС() , у которой имеется родственная ей функция ВСД() , у ЧИСТНЗ() есть функция ЧИСТВНДОХ() , которая вычисляет годовую ставку дисконтирования, при которой ЧИСТНЗ() возвращает 0.
Расчеты в функции ЧИСТВНДОХ() производятся по формуле:
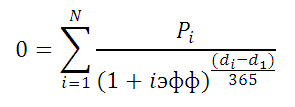
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).
Дисконтирование денежных потоков при оценке эффективности инвестиционных проектов
Метод дисконтирования денежных потоков
Дисконтирование денежных потоков очень актуально для определения наиболее точного значения эффективности инвестиционного проекта. Это обусловлено тем, что стоимость денег со временем меняется, например, под воздействием инфляции. А значит деньги, которые вкладывает инвестор на инвестиционном этапе, будут отличаться от тех денег, которые он получит во время реализации проекта. И чем больше горизонт расчета, тем большие расхождения в стоимости денег возникнут.
И следовательно, для того, чтобы адекватнее оценить эффективность бизнес-проекта, необходимо приведение всех платежей к одному моменту времени. Только в этом случае, у инвестора появляется возможность понять истинную ценность проекта и принять правильное решение.
Одним из способов достижения сравнимости является дисконтирование денежных потоков.
Таким образом, данные методы, в основе которых лежит дисконтирование денежных потоков, являются более точными нежели методы, базирующиеся на расчете простых показателей эффективностит проекта.
Дисконтированные показатели оценки эффективности инвестиционного проекта
Дисконтированные показатели эффективности инвестиционных проектов включают в себя:
- чистый дисконтированный доход (ЧДД, NPV);
- индекс доходности (ДИД, DPI);
- дисконтированный срок окупаемости (Tок, DPР);
- внутренняя норма доходности (ВНД, IRR);
- чистая терминальная стоимость (NTV, ЧТС);
- модифицированная внутренняя норма прибыли (доходности) (MIRR);
- и другие.
Чистый дисконтированный доход (NPV)
Основным показателем при оценке эффективности инвестиций является чистый дисконтированный доход проекта. Именно он показывает в абсолютной величине, сколько принесет проект инвестору.
Суть чистого дисконтированного дохода заключается в следующем. NPV (ЧДД) показывает, на сколько дисконтированные притоки проекта превышают дисконтированные оттоки по нему. То есть данный показатель учитывает то, что стоимость денег меняется во времени.
Чистый дисконтированный доход (NPV) – определяется путем сопоставления величины дисконтированных инвестиций с общей суммой дисконтированных денежных поступлений, порождаемых ими в течение расчетного периода.
По своей сути NPV отражает прогнозную оценку прироста экономического потенциала предприятия в случае принятия рассматриваемого проекта.
Для расчета NPV (ЧДД) используется следующая формула:

Понятно, что, так как NPV — это доход от проекта, то он измеряется в денежных единицах.
Критерий чистого дисконтированного дохода
Для того чтобы принять решение на основе данного показателя, необходимо сравнить полученный NPV с критерием:

 = 0″ title=»Rendered by QuickLaTeX.com» height=»16″ width=»53″ style=»vertical-align: -1px;»>
= 0″ title=»Rendered by QuickLaTeX.com» height=»16″ width=»53″ style=»vertical-align: -1px;»>
Если чистый дисконтированный доход равен 0, то проект окупается. Если NPV больше 0, то инвестиционную деятельность можно осуществлять.
Однако, если чистый дисконтированный доход 0, это вовсе не означает, что инвестор лишь окупит свои инвестиции. Окончательный вывод можно сделать, лишь зная принцип определения ставки дисконтирования. Ведь существуют случаи, когда нулевой чистый дисконтированный доход будет означать, что инвестор получит нормальную прибыль.
Пример расчета чистого дисконтированного дохода (NPV) при постоянной ставке дисконтирования

Рассмотрим на примере, как определить чистый дисконтированный доход проекта и по его значению принять решение об эффективности проекта.


Следовательно, на основе полученных результатов примера, можно сделать вывод, что инвестор сможет окупить свои вложения и получить дополнительно 246916,19 рублей.
Пример расчета чистого дисконтированного дохода (NPV) при изменяющейся ставке дисконтирования
Необходимо обратить внимание на то, что если для каждого расчетного периода задана своя норма дисконта, то использование формулы не возможно. Это происходит из-за того, что деньги теряют свою стоимость не равномерно.
Рассмотрим это на предыдущем примере. Но ставка дисконтирования в этом случае будет изменяться.



Индекс доходности (DPI)
Не смотря на то, что показатель чистый дисконтированный доход, несомненно, имеет целый ряд преимуществ, но он имеет и существенный недостаток.
Этот недостаток заключается в том, что по показателю NPV (ЧДД) нельзя сравнить эффективность нескольких проектов.
Например, NPV по проекту А составил 1 млн. рублей, а по проекту В — 10 млн. рублей. Это не означает, что проект В однозначно более эффективный. Ведь инвестиционные затраты на проект Б, могут быть намного больше, чем по проекту А.
Для решения этой проблемы необходимо использование относительного показателя. Например, индекса доходности. Данный индекс может рассчитываться, как по каждому отдельному проекту (индекс доходности проекта), так и в целом по всему инвестиционному портфелю (индекс доходности проекта ).
Дисконтированный индекс доходности (DPI) – характеризует доход на единицу инвестиционных затрат и рассчитывается как отношение дисконтированных доходов по проекту к дисконтированной стоимости инвестиций.
Для определения дисконтированного индекса доходности используется следующая формула:


DPI измеряется в долях или, в связи с тем, что это экономический показатель, он может измеряться в рублях на рубль (руб./руб.).
Норма индекса доходности
На основании вышеприведенной формулы показателя можно сделать вывод, что он должен быть больше 1.

 = 1″ title=»Rendered by QuickLaTeX.com» height=»17″ width=»52″ style=»vertical-align: -1px;»>
= 1″ title=»Rendered by QuickLaTeX.com» height=»17″ width=»52″ style=»vertical-align: -1px;»>
Таким образом, если полученное значение дисконтированного индекса доходности:
- больше 1, то проект приемлем;
- меньше 1, то инвестиции не оправданы.
Пример расчета индекса доходности (DPI)


Вывод: первый проект имеет больший индекс доходности, следовательно, он более привлекателен, так как более эффективен. В то же время оба проекта приемлемы.
Дисконтированный срок окупаемости (DPР)
Дисконтированный срок окупаемости (DВР) – период, по окончанию которого первоначальные инвестиции покрываются дисконтированными доходами от осуществления проекта.
Таким образом, для определения дисконтированного срока окупаемости используется слудующее неравенство.

DPP определяется также как и PP двумя способами:
- соотношением суммарного объема инвестиций со средними значениями дохода по проекту;
- сопоставления денежных притоков и оттоков по периодам. Это белее точный способ.
Критерий эффективности проекта на основе DPP
Для того чтобы инвестиционный проект был приемлем, необходимо чтобы выполнялось следующее условие:
 T.» title=»Rendered by QuickLaTeX.com» height=»16″ width=»107″ style=»vertical-align: -1px;»>
T.» title=»Rendered by QuickLaTeX.com» height=»16″ width=»107″ style=»vertical-align: -1px;»>
Следовательно, дисконтированный период окупаемости должен быть больше горизонта расчета по проекту.
Внутренняя норма доходности (IRR, ВНД)
Еще одним показателем эффективности проекта является внутренняя норма доходности (IRR, ВНД). На основании расчета IRR инвестор может определить не только эффективнее проект или нет, но и какой запас прочности у него.
Внутренняя норма доходности (IRR, ВНД) – это ставка дисконтирования, при которой проект становится безубыточным, т. е. NPV = 0.
Формула для расчета внутренней нормы доходности (IRR, ВНД) имеет следующий вид:

Критерии внутренней нормы доходности проекта (IRR, ВНД)
Для принятия решения об эффективности проекта на основе внутренней нормы доходности производится ее сравнение со ставкой дисконтирования принятой по проекту:
- IRR > r => Проект приемлем;
- r = IRR => Проект окупается и приносит минимальную величину нормальной прибыли;
- IRR Проект неэффективен.
Определение внутренней нормы доходности с помощью программы Excel
Для облегчения расчетов ВНД (IRR) очень хорошо можно использовать приложение Excel. В русскоязычной версии Excel есть встроенная функция, позволяющая без труда найти значение внутренней нормы доходности.
Эта функция называется ВСД. Пример ее использование приведен на рисунке.

Как видно из рисунка, проект А имеет IRR(ВНД)=24,20%. В то время как по проекту В IRR(ВНД)=18,80%.
Это позволяет сделать следующие выводы :
- Во-первых, проект А более привлекателен, у него больше доходность, так как по нему больше значение ВНД. Следовательно, он обладает большим запасом прочности.
- Во-вторых, если ставка дисконтирования по первому проекту меньше IRR(ВНД)=24,20%, то проект в целом приемлем.
- В-третьих, если ставка дисконтирования по второму проекту меньше IRR(ВНД)=18,80%, то проект также приемлем.
Графический способ определения внутренней нормы доходности
∆ = (IRR — r) характеризует запас прочности проекта
Рассмотрим на предыдущем примере, в котором внутренняя норма доходности определялась с помощью программы Excel, графический способ ее нахождения.

Если например ставка дисконтирования по проекту выбрана равная 10%, то запас прочности по проекту А составит 14,2%, а по проекту В — 8,8%.
Вычисление внутренней нормы доходности методом линейной аппроксимации

Рассмотрим на примере принципы вычисления ВНД методом линейной аппроксимации. Для этого возьмем проект А, рассматриваемый ранее.
 24,34 %» title=»Rendered by QuickLaTeX.com» height=»34″ width=»680″ style=»vertical-align: -12px;»>
24,34 %» title=»Rendered by QuickLaTeX.com» height=»34″ width=»680″ style=»vertical-align: -12px;»>
Вывод: Как мы видим значения ВНД, полученные тремя этими способами приблизительно равны. Понятно, что наиболее точный способ — это вычисление в программе Excel.
Чистая терминальная стоимость (NTV, ЧТС)
Чистая терминальная стоимость (NTV, ЧТС) – это наращенные чистые доходы на конец периода.
 ,
,
где t – анализируемый период.
Отличие чистой терминальной стоимости от чистой дисконтированной стоимости проекта заключается в том, что при расчете NPV применяется принцип дисконтирования, в то время как при расчете NTV — принцип наращивания.
Данное отличие представлено на рисунке.
Принципы принятия проекта на основе критерия NTV
Принципы оценки эффективности инвестиционного проекта на основе расчета показателя чистой терминальной стоимости (ЧТС, NTV) аналогичны принципам оценки на основе расчета чистого дисконтированного дохода (ЧДД, NPV):
- если NTV > 0, то проект следует принять;
- NTV Пример расчета чистой терминальной стоимости проекта (ЧТС, NTV)

 млн. руб.
млн. руб. Вывод: Проект следует принять, т.к. NTV > 0.
Модифицированная внутренняя норма прибыли (доходности) (MIRR)
Модифицированная внутренняя норма прибыли (доходности) (MIRR) – скорректированная с учетом нормы реинвестиции внутренняя норма доходности.
 ,
,Порядок расчета показателя MIRR:
- рассчитывается дисконтированная сумма всех оттоков;
- рассчитывается наращенная стоимость всех притоков (терминальная стоимость);
- определяется ставка, которая уравнивает суммарную текущую стоимость оттоков и наращенную стоимость притоков. В случае если наращенная стоимость притоков превышает дисконтированную стоимость оттоков, такая ставка найдется и будет единственной.
Критерий модифицированной внутренней нормы прибыли (доходности)
Инвестиционный проект считается приемлемым, если:
 r.» title=»Rendered by QuickLaTeX.com» height=»16″ width=»118″ style=»vertical-align: -1px;»>
r.» title=»Rendered by QuickLaTeX.com» height=»16″ width=»118″ style=»vertical-align: -1px;»>Пример расчета MIRR
Рассмотрим на примере принцип расчета модифицированной внутренней нормы рентабельности (MIRR). В данном примере показано, что при вычислении MIRR используется одновременно наращение и дисконтирование денежных потоков.


Дисконтирование денежных потоков широко используют разработчики бизнес-планов. Это позволяет им произвести оценку эффективности с учетом инфляции и других факторов, влияющих на показатели.
http://excel2.ru/articles/chistaya-privedennaya-stoimost-npv-chps-i-vnutrennyaya-stavka-dohodnosti-irr-vsd-v-ms-excel
http://investolymp.ru/diskontirovanie-denezhnyh-potokov-pri-oczenke-effektivnosti-investiczionnyh-proektov.html


